Diffraction Patterns

What is Diffraction?

Diffraction is a phenomena unique to waves. When a wave passes through a gap or travels around an obstacle, it spreads out. All waves can be diffracted, and diffraction doesn't affect the speed, wavelength or frequency.

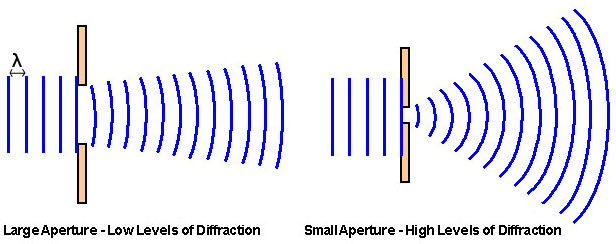
The diagram below illustrates this. When the wavelength of the wave is close to the aperture (size) of the gap, then it diffracts more. On the other hand, when the wavelength is a lot smaller, it doesn't diffract as much.

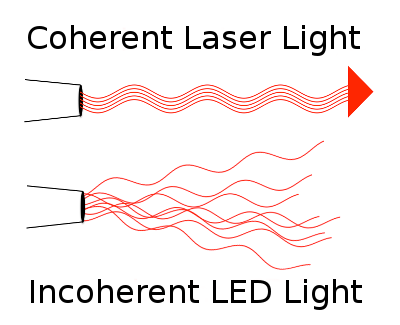
Coherent light

Coherent light is light where phase difference is constant throughout the whole wave.

Interference and Patterns

Remember constructive and destructive interference? Well, imagine coherent light being shone through two small slits. The light diffracts as it passes through the gaps, and when the two diffracted waves interact they interfere constructively and destructively. This leaves regions of high intensity light and other regions where there is no light at all. If you were to place a screen in front of this, you may see the following pattern:

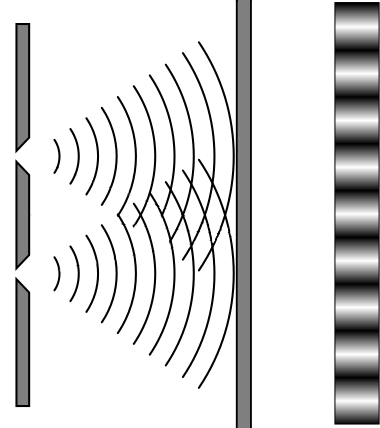
The diffracted waves interfere with one another, leaving the pattern on the screen on the far right.

This is, in essence, Thomas Young's double slit experiment. The experiment proved that light acted as a wave, since only waves can diffract. If light acted as particles, like Newton theorised, then you would see two lines on the screen, directly in front of the slits.

The Diffraction Pattern

The areas of light on the diffraction pattern are called maxima, whereas the areas of dark are called minima. These are labelled from the centre outwards - for instance, the central bright spot is called the central (or zeroth order) maxima, and the ones next to that are called 1st order maximas, then 2nd order, and so on.

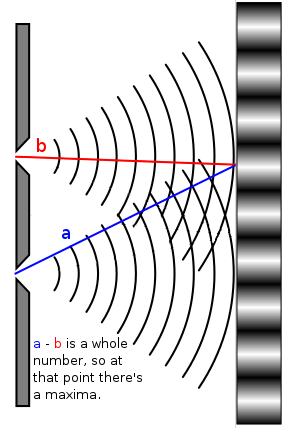
Path difference is the difference between the distance travelled by two waves. If the path difference is zero or a whole number, then the two waves have arrived in phase with one another. This results in constructive interference and a maxima on the screen. If the path difference is an odd number of half wavelengths, then they will be in antiphase, and cancel each other out. This results in destructive interference and a minima on the screen. In the following diagram, a and b represent the distance travelled by two waves from either slit.

The Diffraction Equation

This equation applies to Young's double slit experiment, and you will need to know how to use it for the exam.

λ=^ax⁄_D

wavelength (m) = ^{slit separation (m) x fringe separation (m)}⁄_{distance to screen (m)}